身处这个行业,许多人都是学习的爱好者。但是如何学习,这是一个值得仔细讨论的问题。我遇到最多的问题是:“我做的基本都是业务功能,计算机理论有什么用?” 这个问题常常又和下面这类质疑联系在一起,就更让人困惑。所以今天我想来个现身说法,讲讲计算机理论对做业务到底有什么用。
计算机科学理论到底有什么用呢?我一开始也很困惑这些问题,在学校学数据结构、离散数学等等,总觉得和使用的那些炫酷软件相差万里,似乎人家都腾云驾雾了,自己还在地上修理地球。
某一天在图书馆在做离散数学习题,我感到了“电光火石的瞬间”,原来解决问题可以不靠直觉和猜测,而是有一整套方法。
过河问题,我们小时候都做过:河这边有人、羊、狼、草。如果没有人看着,羊会吃草,狼会吃羊。大家都要过河,但只有一条船,船上每次最多装两样东西。要怎么过河?
我只记得小时候做过这种题,但已经完全不记得是怎么解的了。让我用计算机来解的话更是一头雾水,我完全想不通为什么这个题目和离散数学有什么关系?直到翻看答案才恍然大悟。
人、羊、狼、草,一共四种生物,一开始它们在河这边,最终要去河那边。如果我们换个角度看,每个时刻(不包括渡河中间态),每种生物都可能有两种状态:要么没有渡河,要么已经渡河。如果我们对二进制非常熟悉,就可以迅速穷举出所有的状态(没有渡河标为0,已经渡河标为1)。
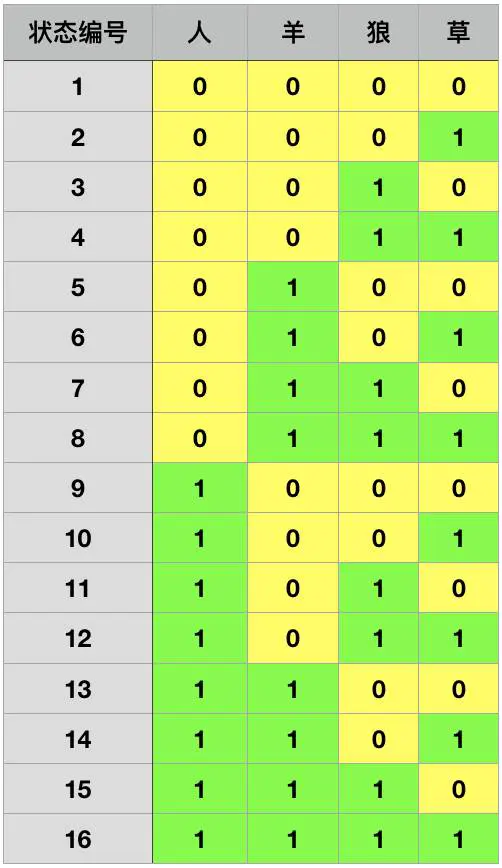
所以,我们要做的其实是从「状态1」出发,抵达「状态16」。我们不妨把每个状态看成一个节点,如果两个状态之间可以通过一次渡河解决,就添加一条边把这两个节点连起来。比如一开始大家都没有渡河(状态1),人和羊可以一次渡河过去(状态13),那么「状态1」和「状态13」两个节点就可以用边连起来。然后人单独乘船回来,那么回到「状态5」,所以「状态13」和「状态5」之间又有一条边相连……
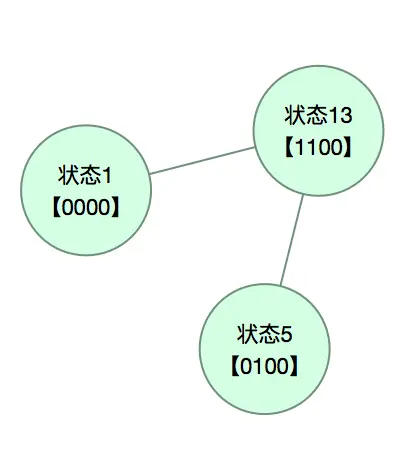
如果从计算机科学的角度来看,这个问题就变成了图中两个节点的连通可达问题。我相信,到了这个程度,大部分人都可以写出程序来解决了。之前之所以解不出,缺的就是计算机科学理论的那点思维。遗憾的是,我见过的大部分计算机教材都没有“点透”,所以尽管学了课程,还是缺那点视角。
我猜,有些人看到这里还不会服气,毕竟这个题目本身也很“理论”。那么好,我们再看看其它的例子。
学过计算理论,或者深入了解过正则表达式的人,一定听说过“自动机”的概念。它由一系列状态和若干转移函数组成。转移函数是这样的一系列规则:从状态q0,输入a,达到状态q1。状态里有两个要特别注意:起始状态,结束状态(下面的图里,q0可以视为起始状态,q3是结束状态)。
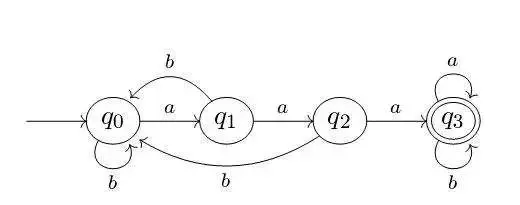
传统的计算机教材讲到自动机,通常也会举个例子:自动售货机。投钱进去,点要买的东西,出货,改变余额…… 最终状态是钱都花光了,或者是退剩下的金额。但是,也就讲到这个例子为止了。看起来,这套理论也那么“理论”,和实际没什么关系。但是,不做自动售货机的业务,真的就可以和自动机划清界限了吗?
我不知道你是否做过订单系统,或者至少了解、思考过。如果都没有也不要紧,你至少应该在网上下过订单。回头想想,知道订单的处理流程会有许多环节(确认、付款、发货、收货、评价……)。那么,它和自动机有关系吗?
我见过不少人,或许是不懂,或许是不屑,觉得这个问题自己很容易搞定——订单的处理无非是一系列状态而已,弄个枚举值,每个状态编个号嘛。然后,真的就这么去这么弄了。一开始确实没问题,随着业务的逐渐负责,问题就来了:需要新增或者删除状态,如何保证各个状态的融洽一致?业务规则不断变化,如何避免有些订单走入了预料不到的死胡同?我就见过好几个历史悠久的订单系统,充斥着大量繁杂的 IF-ELSE 判断,基本处于“谁也不想维护,谁也不敢维护”的状态。
如果换个角度,从自动机的模型出发,就清楚了很多。
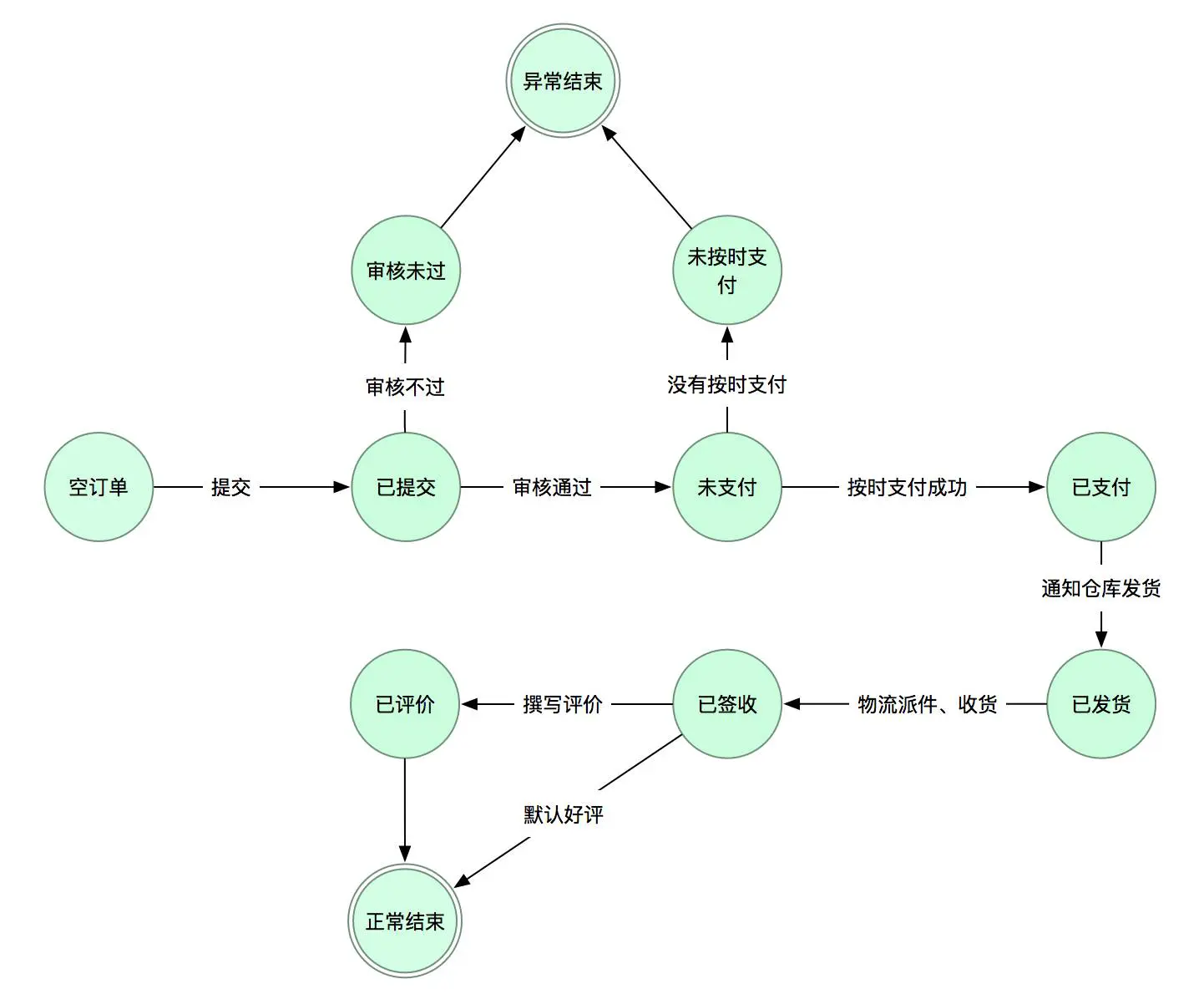
仔细观察,你会发现自动机模型很好地实现了解耦:状态是静态的,我们只要关心它所代表的意义就足够。转移函数负责动态,但它只需要关心“做了什么,结果如何”。而且,所有的状态可以汇总到一张表,所有的转移函数也可以汇总到一张表。再加上一台“不论你是谁,忠实查找转移函数更新状态”的引擎,总共两张表、一台引擎就可以包含所有的信息,干净利落,不留死角。
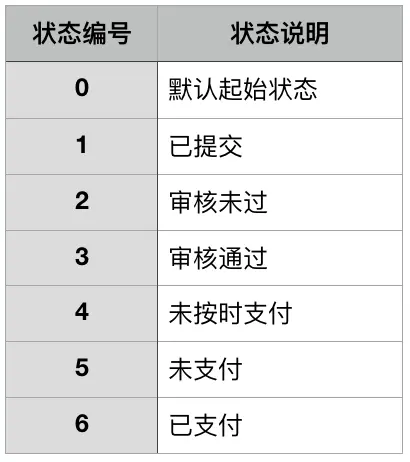
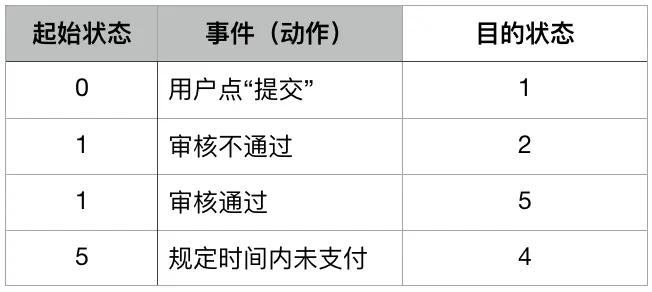
我们都知道,计算机要解决的很多问题之所以难,都是因为过于复杂,所以无论是系统设计、程序设计、算法设计,关键问题都在于降低复杂性,而降低复杂性的有效办法之一就是“分而治之”。用自动机的视角来看待订单问题,恰恰做到了动静分离、责任内聚,很方便分而治之。无论订单处理流程如何变化,无非也是增减两张表的数据而已,状态转移引擎完全不必更改。这样做出来的订单系统,再复杂也不怕。
同样的理论还可以用在更多的领域。比如,我司(沪江)的用户中心在设计在线系统时,也用到了这套理论:所有的在线用户会话总会处于某种状态(可信、不可信、高风险、低风险……),随着用户行为的不断发生,当前会话会在不同的状态之间转移、跃迁。于是,当用户要进行某些关键操作的时候,只要看看当前会话的状态,就可以确定操作是否安全。因为理论模型非常清楚易懂,静态的状态和动态的转移函数责任清晰、职责分明,所以完全拍胸脯说,任何时刻、任何用户会话都处在完全的掌握之中,理解、维护都特别方便。
如果这些例子不能够说服你,最后我们来看一个更高阶的,来自我的朋友J的例子,它应当足够有说服力了。
J同学遇到过这么一个问题:他维护的是数据仓库,你可以把数据仓库设想成一张很大很大的表,有很多很多行(数据条目),很多很多列(数据字段)。数据仓库的查询API成一次只能指定少量条目和少量字段。
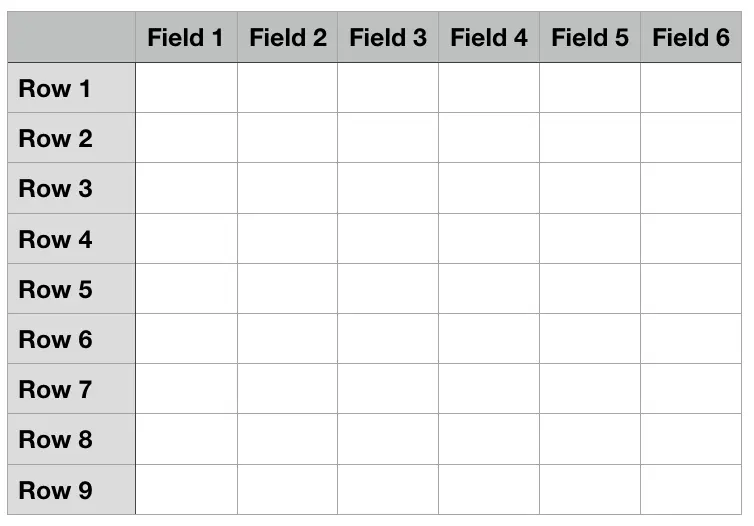
查询是众多类似这样的组合:
-
{(Row1, Row5): (Field3, Field7)}
-
{(Row2): (Field2, Field4)}
-
{(Row3): (Field3, Field5)}
-
{(Row4): (Field2, Field8)}
-
{(Row6): (Field4)}
简单来看似乎没有什么问题,但随着业务增加,这个API就成了瓶颈:业务方往往给出大量「条目-字段」的组合,需要尽快得到答案。数据仓库的查询速度本身没有问题,但启动一次查询的成本很高。
通常大家都会想到异步,一次接收多个请求,查询完成再批量返回。异步会有帮助,但还无法解决性能瓶颈:如何能用尽可能少的查询,得到所有需要的数据。许多人会想到缓存,但简单缓存是行不通的,表太大了,哪怕仅仅缓存一行或者一列的完整数据,也超出了内存的限制。
怎么办呢?幸好我这个朋友的算法学得相当好。他一眼就看出来,这个问题和二部图密切相关。
所谓二部图,指的是这样的图:(我避免使用过于“数学化”的描述)可以把图中所有顶点分为两部分,保证任何一条边关联的两个顶点都在不同的部分。
如果我们从图的角度来看,这个问题天然就是二部图:一个顶点集是要查询的所有条目,另一个顶点集是要查询的所有字段,所有的查询都视为边,边都是是「条目-字段」的组合,因此所有的边都满足“一个顶点在这边,一个顶点在那边”的要求。
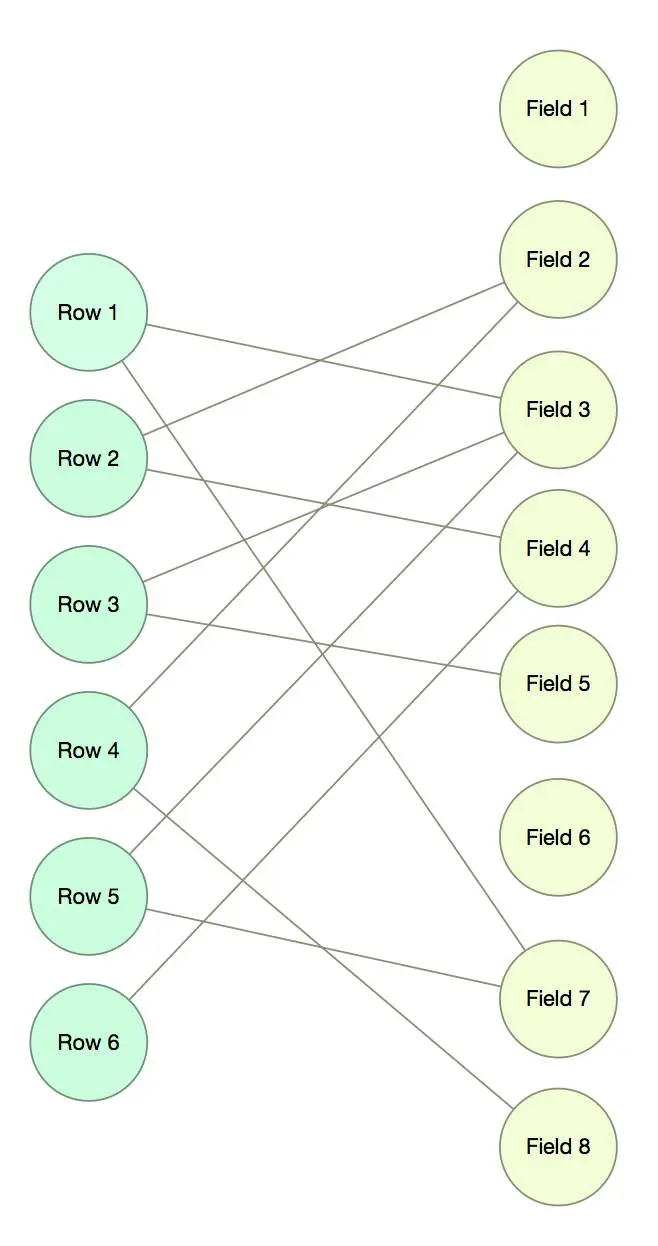
剩下的事情还是分而治之:如何把这个图切分为多个互相隔离的部分?或者说,如何用完全二部图去“覆盖”原来的图?上面说的“切分”其实相当于对零散查询的归并,把海量的零散查询归并为少数集中的查询,既能降低查询次数,又避免了缓存浪费。网上搜索Covering Graphs with Few Complete Biparties Subgraphs,现成解法相当多。上面的图,切分之后就很直观了。
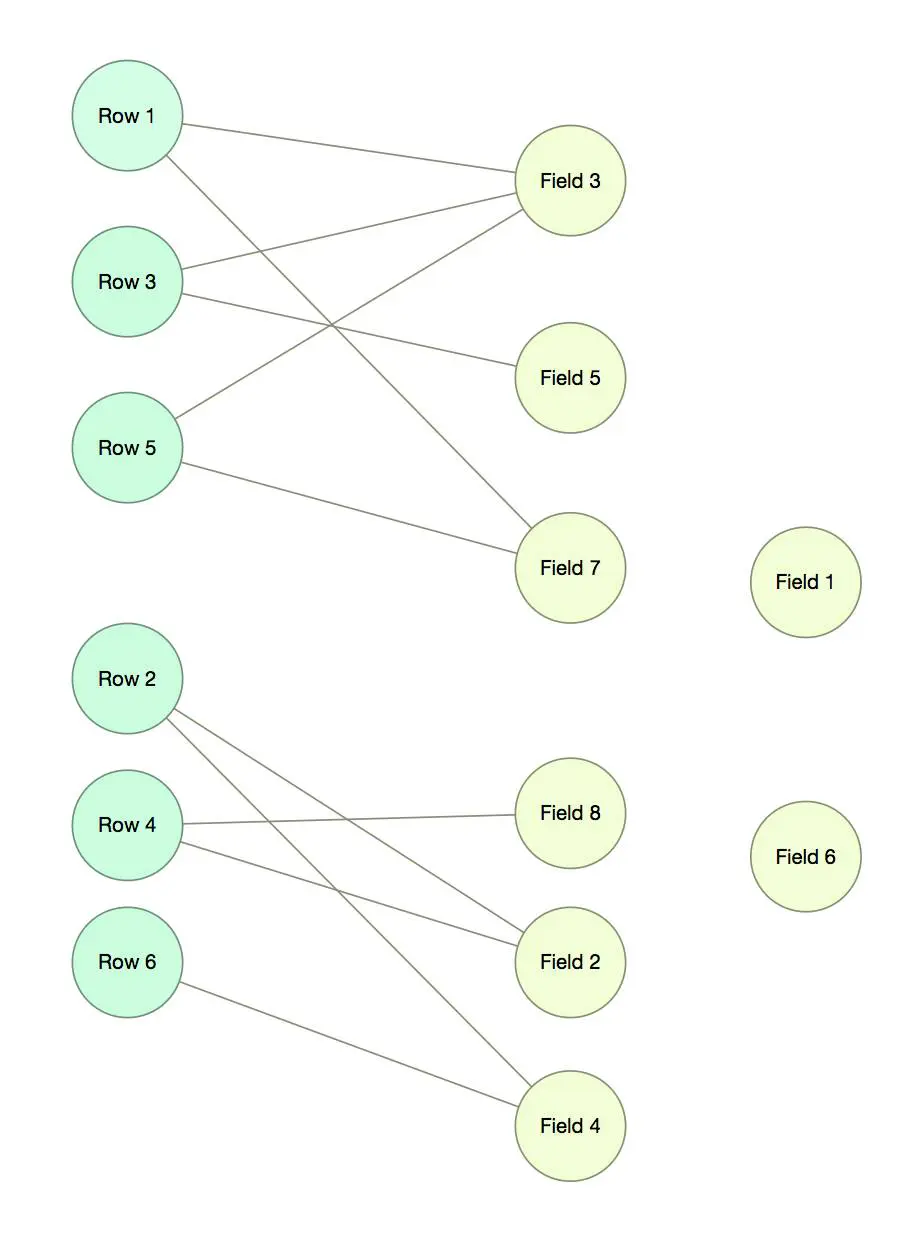
只需要对数据仓库做两次查询,结果集就已经涵盖了所有的查询,而且浪费的空间非常少,时间和空间效率都非常高。
-
{(Row1, Row3, Row5): (Field3, Field5, Field7)}
-
{(Row2, Row4, Row6): (Field2, Field4, Field8)}
难吗?似乎不难理解啊。但是如果没有想到问题的原型,任凭你再会编程,也难找到好的解法。要补充的是,我的这个朋友并不是程序员,他的工作是在金融行业设计数据产品……
上面举了这么多例子,目的是希望给广大不重视算法的程序员朋友们一点启示,一点不一样的思考——其实大家也可以反过来想,你多懂一点点理论,有时候就掌握了哪怕多写几万行代码、多掌握几十种框架也解决不了的问题,何乐而不为?
对了,最后还有个问题。有许多人问:数据仓库提供这么坑爹的API,到底是谁缺心眼设计的?答案是:不知道是谁设计的,但学校里没有《API设计》这门课,真是害人不浅啊~~
我以前写过一篇《 你知道33进制吗?》,也是关于这个主题的,有兴趣的读者可以看看。如果你也遇到过类似的例子,欢迎留言。
