我们说1.0的视力，是说最小分辨角为1分，1分=1/60角度。如果说空间频率，那么应当是一个周期，对于视标来说，就是一黑一白，那么就是2分视角，所以一个周期是2分视角，那么1度之内就应当有30个周期，所以如果以周期/度为单位，1.0视标对应的空间频率就是30周/度。

但如果单位是线/mm，或者周期/mm呢？比如在计算MTF的时候，光学软件很可能提供的单位是线/mm，那么应当是多少？

我们来进行一番推导

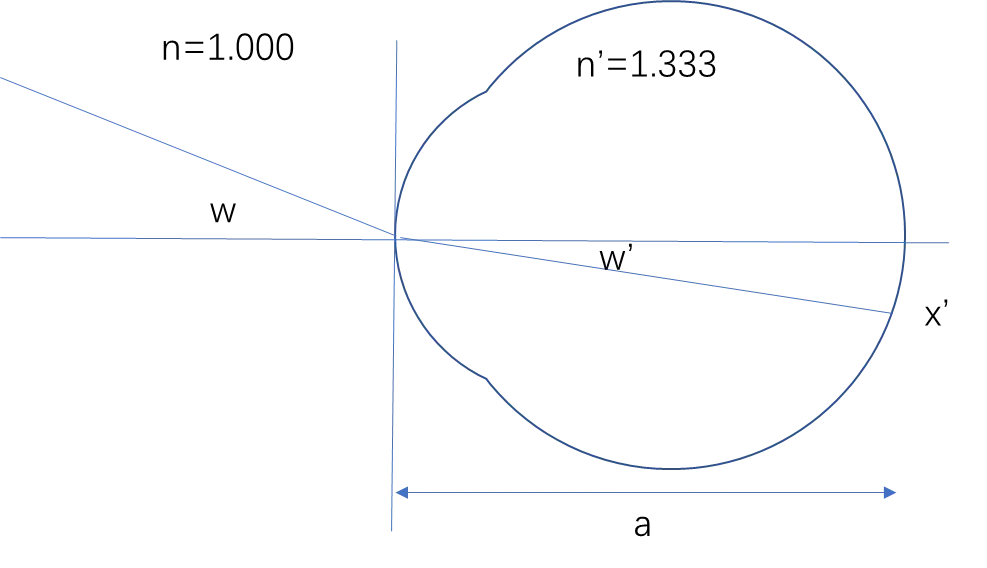
An image to describe post 1.0视标在视网膜上的空间频率是多少？

已知：

  • 当𝛼很小时，sin⁡(𝛼)≈𝛼, tan⁡(𝛼)≈𝛼
  • 如果入射角为w，折射角为w'，那么有折射定律：n sin⁡(𝑤)=𝑛′ sin⁡(𝑤′)

所以：

  • 当入射角w很小时，有近似的折射定律： nw= n’ w’
  • w' = n w/ n' (公式1)

由图中可知

  • 如果在视网膜上的成像高度是x'，眼轴长为a，那么折射角：tan(w’) = -x’/a
  • 当角度很小时，tan⁡(w’)≈w’

所以

  • w’=-x’/a (公式2)

根据公式1和公式2

  • w’ = n w/n’
  • w’ = -x’/a
  • 有n w/n’= -x’/a
  • 代入n=1，得到
  • x‘ = - w a / n’ (公式3)

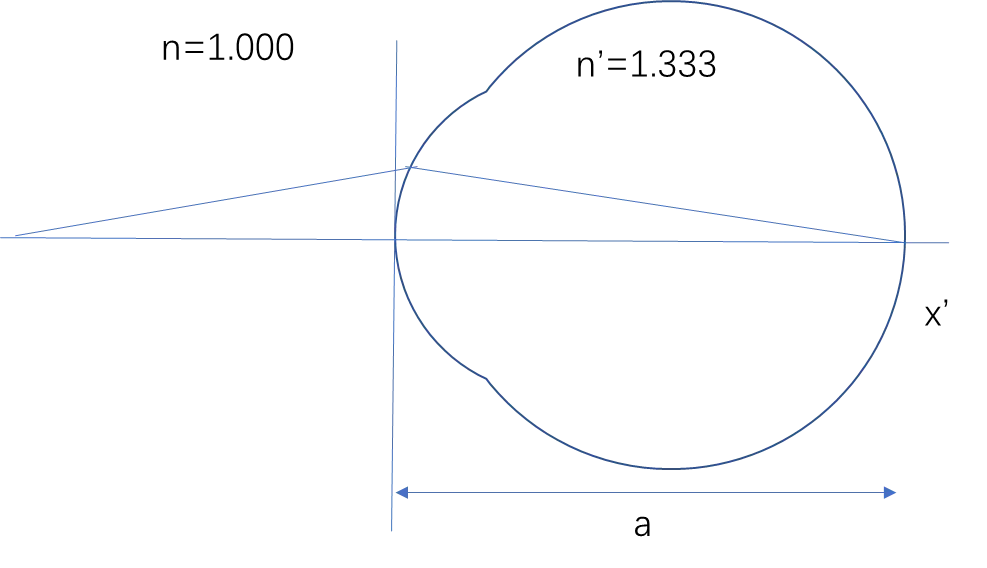
An image to describe post 1.0视标在视网膜上的空间频率是多少？

根据定理
出射光聚散度=入射光的聚散度+界面屈光度

  • 考虑简化眼的角膜，设定出射光的聚散度=A，入射光的聚散度=F_fp，
  • 简化眼的屈光力都在角膜上=F_eye
  • 那么：𝐴=𝐹_𝑓𝑝+𝐹_𝑒𝑦𝑒 (公式4)

根据聚散度的定义

  • A=1.333/a，a=眼轴长度，代入公式4
  • 1.333/a= 𝐹_𝑓𝑝+𝐹_𝑒𝑦𝑒 （公式5）

An image to describe post 1.0视标在视网膜上的空间频率是多少？
根据公式3和公式5

  • x‘ = - w a / n’ (公式3) (n'=1.333)
  • 1.333/a= 𝐹_𝑓𝑝+𝐹_𝑒𝑦𝑒 （公式5）
  • 可以得到 x' = -w a /1.333 = - w /( 1.333/a) = -w / ( 𝐹_𝑓𝑝+𝐹_𝑒𝑦𝑒 ) (公式6）

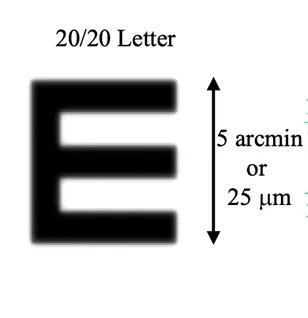
An image to describe post 1.0视标在视网膜上的空间频率是多少？

代入数据到公式6

  • w是最小分辨角的2倍，w=1/30 度，换算成弧度
  • 𝑤=1/30 𝑑𝑒𝑔𝑟𝑒𝑒=1/30∗𝜋/180=5.8×10^(−4) 弧度
  • 正视眼，F_fp=0，F_eye=60D
  • 代入公式6
  • x’ = 5.8×10^(−4)/60≈6×10^(−4)/60=10^(−5) 米=10^(−2) mm

也就是说视标上一黑一白在视网膜上的成像高度是0.01mm，那么每毫米就有1mm/0.01mm = 100周期。

所以，1.0视标对应的空间频率是100线/mm，或者100周/mm。