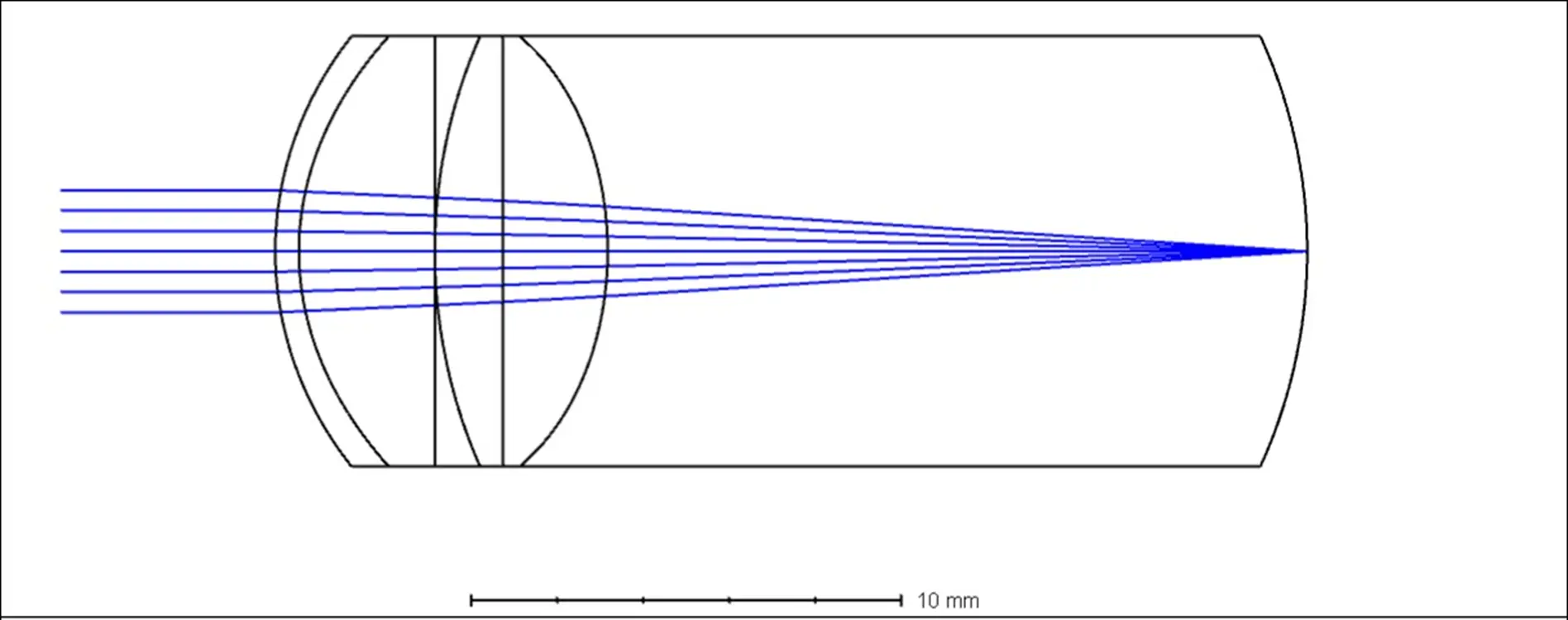
When we say a visual acuity of 20/20, we mean the minimum resolution angle is 1 minute, where 1 minute is equal to ( \frac{1}{60} ) degrees. In terms of spatial frequency, it should represent one cycle. For a optotype, which consists of one black and one white, it represents a 2-minute angle. Thus, one cycle is a 2-minute angle, meaning there should be 30 cycles within 1 degree. So if the unit is cycles/degree, the spatial frequency corresponding to a 20/20 optotype is 30 cycles/degree.
But what if the unit is lines/mm, or cycles/mm? For instance, when calculating the MTF, optical software might use the unit lines/mm. How much would that be?
Let's derive it.
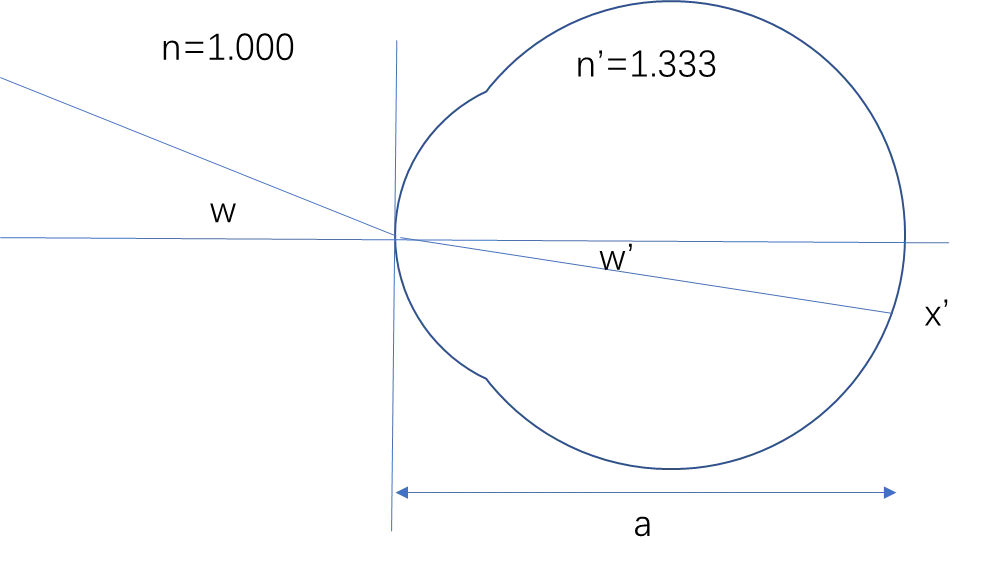
Given:
- When ( \alpha ) is small, ( \sin(\alpha) \approx \alpha ), ( \tan(\alpha) \approx \alpha )
- If the angle of incidence is ( w ) and the angle of refraction is ( w' ), then by the law of refraction: ( n \sin(w) = n' \sin(w') )
Therefore:
- When the angle of incidence ( w ) is small, an approximate law of refraction is: ( nw = n' w' )
\[w' = \frac{n w}{n'} \]
(Formula 1)
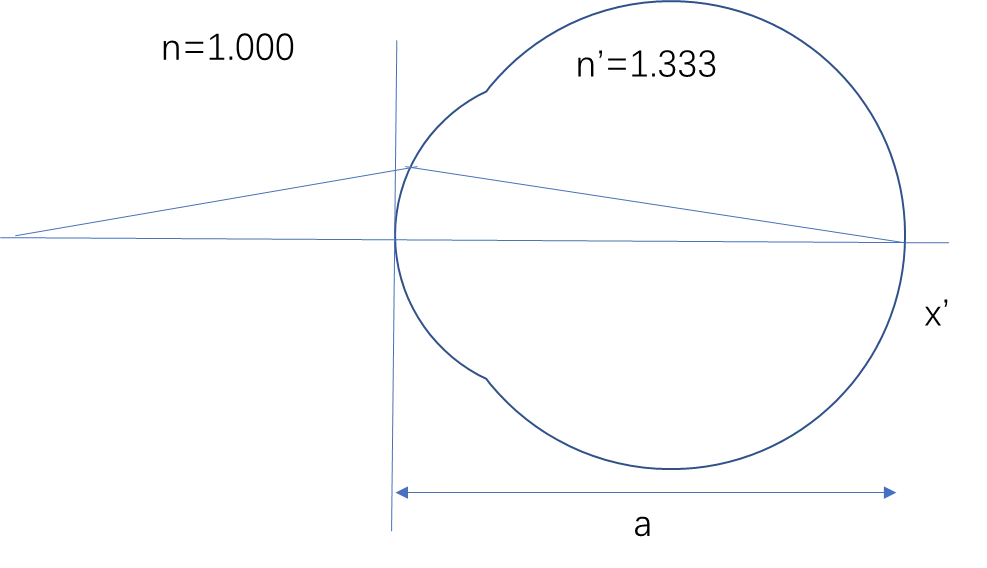
From the diagram:
- If the image height on the retina is ( x' ) and the length of the eye axis is ( a ), then the angle of refraction is ( \tan(w') = -\frac{x'}{a} )
- When the angle is very small, ( \tan(w') \approx w' )
So:
-
\[ \]
According to Formula 1 and Formula 2:
- ( w' = \frac{n w}{n'} )
- ( w' = -\frac{x'}{a} )
- Thus, ( \frac{n w}{n'} = -\frac{x'}{a} )
- Substituting ( n = 1 ), we get:
-
\[ \]
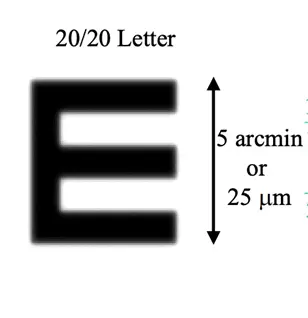
According to the theorem:
The divergence of the outgoing light = the divergence of the incoming light + the refractive power of the interface
- Considering a simplified cornea of the eye, let the divergence of the outgoing light be ( A ), the divergence of the incoming light be ( F_{fp} ),
- The refractive power of the simplified eye is all on the cornea ( F_{eye} )
- Then: \(A = F_{fp} + F_{eye}\) (Formula 4)
According to the definition of divergence:
- ( A = \frac{1.333}{a} ), where ( a ) is the length of the eye axis. Substituting into Formula 4:
-
\[ \]

Based on Formulas 3 and 5:
- ( x' = -\frac{w a}{1.333} = -\frac{w}{\frac{1.333}{a}} = -\frac{w}{F_{fp} + F_{eye}} ) (Formula 6)
Substituting values into Formula 6:
- ( w ) is twice the minimum resolution angle, ( w = \frac{1}{30} ) degree, converted to radians:
- ( w = \frac{1}{30} \times \frac{\pi}{180} = 5.8 \times 10^{-4} ) radians
- For emmetropic eyes, ( F_{fp} = 0 ), ( F_{eye} = 60D )
- Substituting into Formula 6:
- ( x' = \frac{5.8 \times 10^{-4}}{60} \approx \frac{6 \times 10^{-4}}{60} = 10^{-5} ) meters = ( 10^{-2} ) mm
This means that the image height of one black and one white on the retina of the optotype is 0.01mm. Thus, there are ( \frac{1 \text{mm}}{0.01 \text{mm}} = 100 ) cycles per mm.
Therefore, the spatial frequency corresponding to a 20/20 optotype is 100 lines/mm or 100 cycles/mm.