用wolfram语言和python对隐函数求N阶导数

例题：

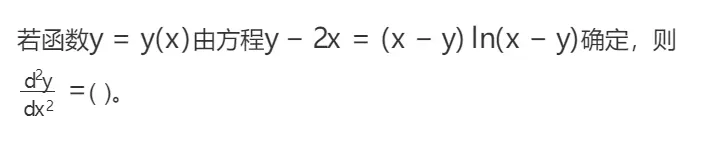
要求解隐函数求导，就是对方程两边同时对x求导，但是要注意y是x的函数，所以不能把y当作常数处理了，而是需要使用链式法则。

手工求解一阶导数

等式右边

先手工演示右边的求导：

当求导表达式 \((x - y)\log(x - y)\) 对于 \(x\) 时，其中 \(y\) 是 \(x\) 的函数，我们需要应用乘积法则和链式法则。这里是一步一步的过程：

1. 应用乘积法则:
   对于形式为 \(u \cdot v\) 的函数的导数，其中 \(u\) 和 \(v\) 都是 \(x\) 的函数，其导数是 \(u'v + uv'\)。在我们的例子中，\(u = x - y\) 且 \(v = \log(x - y)\)。我们需要分别对 \(u\) 和 \(v\) 求导。

2. 对 \(u\) 求导:
   \(u = x - y\)。因此，\(u'\)（对 \(x\) 的导数）是 \(1 - y'\)，其中 \(y'\) 是 \(y\) 对 \(x\) 的导数。

3. 对 \(v\) 求导:
   \(v = \log(x - y)\)。使用链式法则，我们先对内函数 \(x - y\) 求导，得到 \(1 - y'\)。然后乘以外函数 \(\log(z)\) （其中 \(z = x - y\)）的导数 \(\frac{1}{z}\)。所以，\(v'\) 是 \(\frac{1 - y'}{x - y}\)。

4. 组合这两个导数:
   根据乘积法则，总导数是 \(u'v + uv'\)。代入 \(u'\) 和 \(v'\) 的值，我们得到：

   \[(1 - y') \log(x - y) + (x - y) \frac{1 - y'}{x - y} \]

5. 简化表达式:
   简化上述表达式，我们可以合并项并化简。

最终的导数表达式是：

\[(1 - y') \log(x - y) + 1 - y' \]

这就是对 \((x - y)\log(x - y)\) 对 \(x\) 求导的结果，其中 \(y\) 是 \(x\) 的函数。

等式左边

比较容易，对y-2x，一眼看出结果是 y'-2

求解y'

将等式两侧联立，然后把y'当作是一个未知数，求解出来

\[y'-2=(1 - y') \log(x - y) + 1 - y' \]

得到

\[y'=\frac{\log (x-y)+3}{\log (x-y)+2} \]

用wolfram求解一阶导数

在Wolfram语言中，求导使用D[f[x],x]，但我们需要明确告知wolfram，y不能当作常数处理了。

equation=(y-2x==(x-y)Log[x-y])
D[equation,x,NonConstants->y]

结果：

可以看出，Wolfram把y'，写成了D[y,x,NonConstants->{y}]，如果看着很别扭的话，可以用 /.D[y,x,NonConstants->{y}]->y' 来简化

所以我们可以使用

equation=(y-2x==(x-y)Log[x-y])
Solve[D[equation,x,NonConstants->y]/.D[y,x,NonConstants->{y}]->y', y']

得到

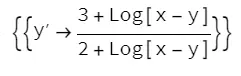
用Python求解一阶导数

用Python求解时，也需要显式声明y是x的函数。

在下面的代码段中，这一段是关键部分：

x = symbols('x')
y = symbols('y', cls=Function)
y = y(x)

1. x = symbols('x') 创建了一个符号变量 x。

2. y = symbols('y', cls=Function) 创建了一个符号函数 y。这表示 y 是一个函数，它可以接受参数（例如 x）。

3. y = y(x) 实际上是在定义 y 为 x 的函数。在这里，y 不再是一个单独的符号，而是一个关于 x 的函数，即 y(x)。

from sympy import symbols, Function, Eq,log,solve, simplify

# 定义 x 和 y 为符号变量
x = symbols('x')
y = symbols('y', cls=Function)
y = y(x)
equation = Eq(y-2*x, (x-y)*log(x-y))
# 对方程关于 x 求导，使用链式法则
diff_eq = equation.lhs.diff(x) - equation.rhs.diff(x)

# 解出 dy/dx
dy_dx = solve(diff_eq, y.diff(x))[0]

也可以得到结果：

用wolfram求解二阶导数

硬来也是可以的，我们先观察对等式两边求二阶导

equation=(y-2x==(x-y)Log[x-y])
D[equation,{x,2},NonConstants->y]

的结果

可以看到，里面有两个很复杂的东西：

• D[y,{x,2},NonConstants->{y}]，这相当于是y对x的二阶导数y''(x)
• D[y,x,NonConstants->{y}]，这相当于是y对x的一阶导数y'(x)，这一部分我们之前已经求解过了。所以可以用/.的方法把它替换掉。

于是，可以这样写

equation=(y-2x==(x-y)Log[x-y])
yprime1=Solve[D[equation,{x,1},NonConstants->y],D[y,{x,1},NonConstants->{y}]][[1]]//Simplify
yprime2=Solve[D[equation,{x,2},NonConstants->y]/.yprime1,D[y,{x,2},NonConstants->{y}]][[1]]//Simplify

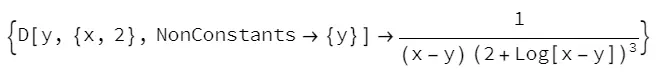
用wolfram对隐函数求N阶导数

如果要求解3阶导数

equation=(y-2x==(x-y)Log[x-y])
yprime1=Solve[D[equation,{x,1},NonConstants->y],             D[y,{x,1},NonConstants->{y}]][[1]]//Simplify
yprime2=Solve[D[equation,{x,2},NonConstants->y]/.yprime1,       D[y,{x,2},NonConstants->{y}]][[1]]//Simplify
yprime3=Solve[D[equation,{x,3},NonConstants->y]/.yprime1/.yprime2, D[y,{x,3},NonConstants->{y}]][[1]]//Simplify

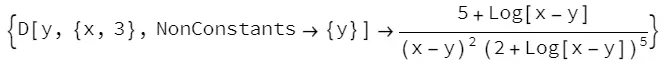
看起来对称优雅，所以只要把替换列表维护起来就可以了。

(* 定义原始方程 *)
equation = (y - 2 x == (x - y) Log[x - y]);

(* 定义一个函数来计算 n 阶导数 *)
DerivativesUpToN[equation_, n_] := Module[
    {
        derivatives = {},
        currentDerivative,
        equationDerivative
    },
    
    (* 对每一个阶数进行迭代 *)
    For[i = 1, i <= n, i++,
        (* 对方程进行 i 阶求导 *)
        equationDerivative = D[equation, {x, i}, NonConstants -> y];

        (* 替换之前所有求得的导数表达式 *)
        equationDerivative = equationDerivative /. derivatives;

        (* 解出当前阶的导数表达式 *)
        currentDerivative = Solve[equationDerivative, D[y, {x, i}, NonConstants -> {y}]][[1]]//Simplify;

        (* 添加到列表中,注意此处要Flatten，否则会出错 *)
        derivatives=Flatten[Append[derivatives,currentDerivative]];

    ];

    (* 返回最后一个导数 *)
    derivatives[[-1]]
]
DerivativesUpToN[equation,4]

用Python求二阶导数

在python上，我们也可以尝试直接从上一步得到的dy/dx中对x求导，

# 定义 x 和 y 为符号变量
x = symbols('x')
y = symbols('y', cls=Function)
y = y(x)
equation = Eq(y-2*x, (x-y)*log(x-y))
# 对方程关于 x 求导，使用链式法则
diff_eq = equation.lhs.diff(x) - equation.rhs.diff(x)

# 解出 dy/dx
dy_dx = solve(diff_eq, y.diff(x))[0]

# 对 dy/dx 关于 x 求导，使用链式法则
d2y_dx2 = dy_dx.diff(x)

# 替换并简化二阶导数的表达式
d2y_dx2_substituted = d2y_dx2.subs(y.diff(x), dy_dx)
d2y_dx2 = simplify(d2y_dx2_substituted)

结果是：

Sympy的simplify功能没有Wolfram那么强，其实是一样的。

用Python对隐函数求N阶导数

仔细观察二阶导数的结果，发现其实里面只有y(x)，没有更复杂的y'(x)或者以上的东西。所以如果我们要求三阶导数，只需要在二阶的基础上再做一次求导，然后替换掉其中一阶导数的结果就可以了。类似的，求N阶导数，在求解了N-1阶导数以后，再求一次导，然后替换掉其中出现的一阶导数。

from sympy import symbols, Function, Eq,log,solve, simplify

def derivative_hidden_function(equation, x, y_func,N):
    # 对方程关于 x 求导，使用链式法则
    diff_eq = equation.lhs.diff(x) - equation.rhs.diff(x)
    # 解出 dy/dx
    dy_dx = solve(diff_eq, y_func.diff(x))[0]
    if N==1:
        return dy_dx
    diy_dxi=dy_dx
    # 对 dy/dx 关于 x 求导，使用链式法则，然后替换一阶导数的结果
    for i in range(N-1):
        diy_dxi = diy_dxi.diff(x).subs(y_func.diff(x), dy_dx)
        diy_dxi = simplify(diy_dxi)
    return simplify(diy_dxi)

# 定义 x 和 y 为符号变量
x = symbols('x')
y = symbols('y', cls=Function)
y = y(x)

# 示例方程
example_equation = Eq(y-2*x, (x-y)*log(x-y))

# 调用函数并显示结果
derivative_hidden_function(example_equation, x, y, 3)

补充

wolfram中，也可以明确把y是x的函数写成y[x] ，下面这样写也是没有问题的：

equation=(y[x]-2x==(x-y[x])Log[x-y[x]])
Solve[D[equation,x],D[y[x],x]]